`ProHVer` Tool Homepage

ProHVer is a tool to handle systems which feature both discrete and continuous behaviour, and also involves randomness. ProHVer is capable of computing the unbounded reachability probability for a very general class of probabilistic hybrid automata. This homepage presents the tool, as well as some case studies on which it was applied.

Authors

ProHVer is under development by Patrick Dubbert and Ernst Moritz Hahn.

Contact/Support

For questions and comments regarding ProHVer, please contact "emh [at] cs [dot] uni [minus] saarland [dot] de".

Tool Architecture

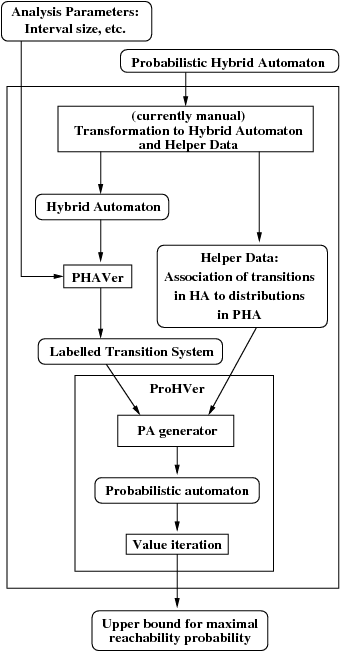
ProHVer works as follows: At first, a probabilistic hybrid automaton description is transformed to a non-probabilistic hybrid automaton description in PHAVer [Frehse05] format (later extensions will involve usage of other hybrid solvers [AlurDI06,RatschanS07,Frehse05]. Additionally, we need to generate some helper data to associate the nondeterministic transitions in the non-probabilistic hybrid automaton with the corresponding distributions in the probabilistic hybrid automaton. Currently, these transformations are done manually, but will be automatized in future versions of ProHVer. The non-probabilistic hybrid automaton is fed into a modified versions of PHAVer. In addition, PHAVer is provided with some informations about the coarseness of the abstraction to be generated, and the like. PHAVer generates an abstract transition system, forming an overapproximation of the non-probabilistic hybrid automaton. Our tool ProHVer combines the labelled transition system with the data associating nondeterministic decisions with distributions, to obtain a probabilistic automaton. This probabilistic automaton is an overapproximation of the original probabilistic hybrid automaton. Using value iteration in this abstraction, ProHVer then computes a probability that is an upper bound for the maximal reachability probability for the property given in the probabilistic hybrid automaton. The theoretical background of the basic technique is described in "Safety Verification for Probabilistic Hybrid Systems", CAV 2010 [ZhangSRHH10]. With an extension of this technique [FraenzleHHWZ11], we can also handle models involving continuous probability distributions by first over-approximating them by discrete ones.

Download and Installation

The latest version of ProHVer can be obtained here. Notice that ProHVer consists of two components. One of them is a modified version of PHAVer which produces a labelled transition system. The other tool reads this labelled transition system, converts it into a Markov decision process and computes bounds on the reachability probability of the original system. Thus, you will need to download both tools.

Compilation

Building the modified version of PHAVer works similar to building the original version of this tool. To build ProHVer, unpack the source archive, go to the directory where it was unpacked and type "make" Beforehand, you may want to activate optimisations in the "Makefile".

Installation

There in no installation routine; once you have downloaded binaries package or compiled the tools from source, you can run them in place. If you wish, you can copy the executables to your bin directory (~/bin as normal user or /usr/bin as root) to make them available system-wide).

Usage

Please type

<phaver> <model.phaver>

Here, <phaver> is the command to execute the PHAVer binary you can download from above, and <model.phaver> is the model under consideration. This command will create a file with the ending .graph, denoted by <result-file.graph>. Let <prohver> be the command for ProHVer. Now, type

<prohver>  <  <result-file.graph>

to obtain a probability. It is the first number in the single line of resulting output.

In case of problems with running the binary or compiling the sources, please contact Ernst Moritz Hahn.

ProHVer Tool Homepage